Asymptotic Notations

sem4 | 0 comments

Asymptotic Notations

  • Asymptotic Notations are methods to estimate and represent efficiency of the algorithm using simple formula
  • To choose the best algorithm we need to check the efficiency of each algorithm.
  • The efficiency of the algorithm can be measured by calculating the time complexity of the algorithm
  • Asymptotic Notations is a short hand wave to represent time complexity

Various Asymptotic Notations

* Big Oh Notation

* Big Omega Notation

*Big Theta Notation

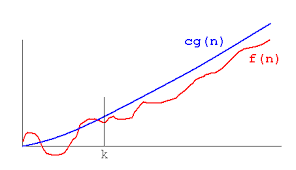
Big O Notation

It is Worst case running time of an algorithm and for the large values of n.

The maximum no. Of steps to solve a problem.

Function t(n) is said to be the O[g(n)].If f(n) is bounded by some constant multiples of g(n) for large values of n,then should satisfy

f(n)<=c[g(n)] where n>=n0.

bigoh

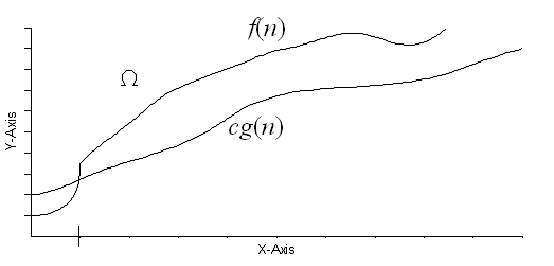
Big Omega Notation

It is the best case efficiency of the algorithm and for large values of n.Minimum number of steps required to solve the problem.

Function f(n) is said to be O[g(n)].If f(n) is bounded by some .positive constant multiples of c[g(n)] for large values of n, then there should satisfy

f(n)>=c[g(n)] where n>n0.

theta

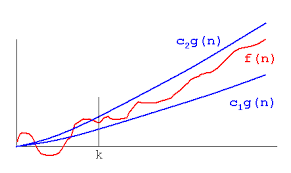
Big Theta Notation

It is the average case efficiency of the algorithm for the large values of n.Average number of steps required to solve the problem.

Function f(n) is said to be O[g(n)].If f(n) is bounded both above and below by constant multiples of c[g(n)] for large values of n,there should satisfy

c1[g(n)] <= f(n) <= c2[g(n)] where n>n0.

thetaa

Little O Notations

The notations is used to describe the worst case analysis and concerned with the small values of n.

A function t(n) is said to be O[g(n)] if there exists some positive constants C.

Little Omega Notation

The notation is used to describe the best case analysis of the algorithm and concerned with the small values of n.A function t(n ) is said to be O[g(n)] if there exists some constants C.

Submit a Comment