Amplitude Shift Keying
Amplitude-shift keying (ASK) is a form of amplitude modulation that represents digital data as variations in the amplitude of a carrier wave. In an ASK system, the binary symbol 1 is represented by transmitting a fixed-amplitude carrier wave and fixed frequency for a bit duration of T seconds. If the signal value is 1 then the carrier signal will be transmitted; otherwise, a signal value of 0 will be transmitted.
Any digital modulation scheme uses a finite number of distinct signals to represent digital data. ASK uses a finite number of amplitudes, each assigned a unique pattern of binary digits. Usually, each amplitude encodes an equal number of bits. Each pattern of bits forms the symbol that is represented by the particular amplitude. The demodulator, which is designed specifically for the symbol-set used by the modulator, determines the amplitude of the received signal and maps it back to the symbol it represents, thus recovering the original data. Frequency and phase of the carrier are kept constant.
Like AM, ASK is also linear and sensitive to atmospheric noise, distortions, propagation conditions on different routes inPSTN, etc. Both ASK modulation and demodulation processes are relatively inexpensive. The ASK technique is also commonly used to transmit digital data over optical fiber. For LED transmitters, binary 1 is represented by a short pulse of light and binary 0 by the absence of light. Laser transmitters normally have a fixed “bias” current that causes the device to emit a low light level. This low level represents binary 0, while a higher-amplitude lightwave represents binary 1.
The simplest and most common form of ASK operates as a switch, using the presence of a carrier wave to indicate a binary one and its absence to indicate a binary zero. This type of modulation is called on-off keying (OOK), and is used at radio frequencies to transmit Morse code (referred to as continuous wave operation),
More sophisticated encoding schemes have been developed which represent data in groups using additional amplitude levels. For instance, a four-level encoding scheme can represent two bits with each shift in amplitude; an eight-level scheme can represent three bits; and so on. These forms of amplitude-shift keying require a high signal-to-noise ratio for their recovery, as by their nature much of the signal is transmitted at reduced power.

ASK diagram
ASK system can be divided into three blocks. The first one represents the transmitter, the second one is a linear model of the effects of the channel, the third one shows the structure of the receiver. The following notation is used:
- ht(f) is the carrier signal for the transmission
- hc(f) is the impulse response of the channel
- n(t) is the noise introduced by the channel
- hr(f) is the filter at the receiver
- L is the number of levels that are used for transmission
- Ts is the time between the generation of two symbols
Different symbols are represented with different voltages. If the maximum allowed value for the voltage is A, then all the possible values are in the range [−A, A] and they are given by:
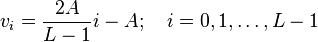
the difference between one voltage and the other is:
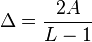
Considering the picture, the symbols v[n] are generated randomly by the source S, then the impulse generator creates impulses with an area of v[n]. These impulses are sent to the filter ht to be sent through the channel. In other words, for each symbol a different carrier wave is sent with the relative amplitude.
Out of the transmitter, the signal s(t) can be expressed in the form:
![s (t) = \sum_{n = -\infty}^\infty v[n] \cdot h_t (t - n T_s)](https://upload.wikimedia.org/math/4/e/6/4e606c68a1e951b87afb54d6c3855ea2.png)
In the receiver, after the filtering through hr (t) the signal is:
![z(t) = n_r (t) + \sum_{n = -\infty}^{\infty} v[n] \cdot g (t - n T_s)](https://upload.wikimedia.org/math/c/5/5/c55aa2b9e20fbaaee735989952df50fb.png)
where we use the notation:
![]()
![]()
where * indicates the convolution between two signals. After the A/D conversion the signal z[k] can be expressed in the form:
![]()
In this relationship, the second term represents the symbol to be extracted. The others are unwanted: the first one is the effect of noise, the third one is due to the intersymbol interference.
If the filters are chosen so that g(t) will satisfy the Nyquist ISI criterion, then there will be no intersymbol interference and the value of the sum will be zero, so:
![z[k] = n_r [k] + v[k] g[0]](https://upload.wikimedia.org/math/f/9/d/f9dcc21216a47dd2158fc78570fcb540.png)
the transmission will be affected only by noise.

