Hooke’s Law
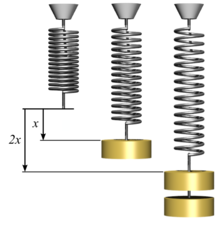Hooke’s law is a principle of physics that states that the force needed to extend or compress a spring by some distance is proportional to that distance. That is: where is a constant factor characteristic of the spring, its stiffness.
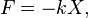where 
is a constant factor characteristic of the spring, its stiffness.
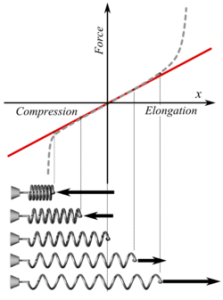
Hooke’s law for a spring is often stated under the convention that 
is the restoring (reaction) force exerted by the spring on whatever is pulling its free end. In that case the equation becomes
since the direction of the restoring force is opposite to that of the displacement.
In SI units, displacements are measured in metres (m), and forces in newtons (N or kg·m/s2). Therefore the spring constant , and each element of the tensor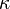 
, is measured in newtons per metre (N/m), or kilograms per second squared (kg/s2).
For continuous media, each element of the stress tensor 
is a force divided by an area; it is therefore measured in units of pressure, namely pascals (Pa, or N/m2, or kg/(m·s2). The elements of the strain tensor 
are dimensionless (displacements divided by distances). Therefore the entries of 
are also expressed in units of pressure.
