Drawing of Tangents and Normals
If you differentiate the equation of a curve, you will get a formula for the gradient of the curve. Before you learnt differentiation, you would have found the gradient威而鋼
of a curve by drawing a tangent and measuring the gradient of this. This is because the gradient of a curve at a point is equal to the gradient of the tangent at that point.
The equation of the tangent to a point on a curve can therefore be found by differentiation.
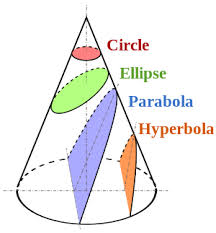
TANGENTS TO AN ELLIPSE
An ellipse is a closed convex curve, therefore a tangent can be drawn to an ellipse at every point on the curve.
Just as every tangent to a circle forms equal angles with the radius at its point of tangency, every tangent to an ellipse forms equal angles with the focal radii of its point of tangency.
Visit Construction of Ellipse to view how to construct normal and tangent
TANGENTS TO A PARABOLA
A tangent to a parabola will always bisect the angle created when the point of contact is joined to the focal point and the directrix.
Visit Construction of Parabola to view how to construct normal and tangent
TANGENTS TO A HYPERBOLA
A tangent to a hyperbola will always bisect the angle created when the point of contact is joined to the focal points.
Visit Construction of Hyperbola to view how to construct normal and tangent