Construction of Ellipse
Sample Problem 1:
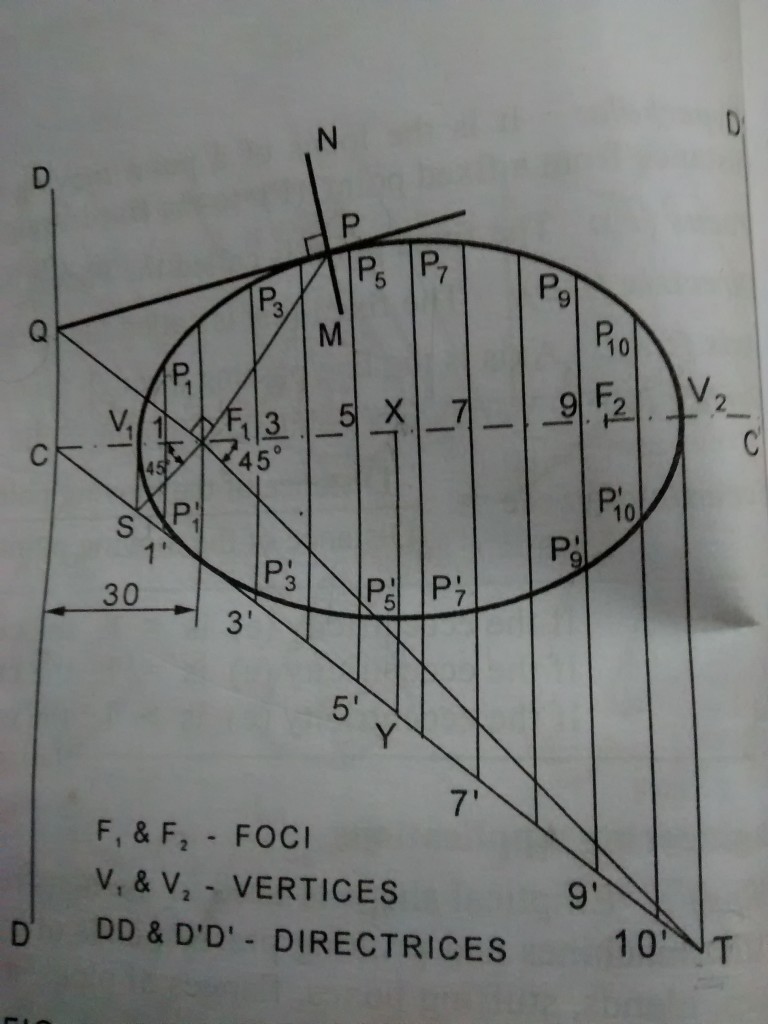
a) Construct an ellipse when the distance between the focus and the directrix is 30mm and the eccentricity is 3/4.
b) Draw the tangent and normal at any point p on the curve using directrix.
Steps for Construction of Ellipse.
Solution: a)
- Draw a vertical line DD to represent the directrix.At any point C on it draw a line perpendicular to the directrix to represent the axis CC’.
- Distance between the focus and the directrix is 30 mm. Hence mark F1, the focus such that CF1=30mm.
- e=3/4. So construct a right angled Δ CXY such that XY/CX = 3units/4units . (X is any point on the axis).
- From F1 draw a 45º line to cut CY at S.From S erect Vertical to intersect CF1 at V1, the vertex. Now SV1 = F1V1.
- ΔCXY is similar to ΔCV1S.
∴SV1/CV1 = XY/CX = F1V1/CV1 = 3/4. - From F1 draw another 45º line to intersect the extension of CY at T. From T erect vertical to intersect the axis at V2, another vertex. V1V2 = Major Axis.
- Along the major axis, mark points 1,2,….,10 at approximately equal intervals. Through these points erect verticals to intersect CY (produced if necessary) at 1′,2′,…,10′.
- With 11′ as radius and F1 as centre draw two arcs on either side of the axis to intersect the vertical line drawn through 1 at P1 and P1′ .
- With 22′ as radius and F1 as centre draw two arcs on either side of the axis to intersect the vertical line drawn through 2 at P2 and P2′ .
- Repeat the above and obtain P3 and P3′,….,P10 and P10′ corresponding to 2,3,….,10 respectively. Draw a smooth ellipse passing through V1,P1,…,P10,V2,P10′,…,P1′,V1.
- To mark another Focus F2: Mark F2 on the axis such that V2F2 = V1F1.
- To mark another Directrix D’D’ : Mark C’ along the axis such that C’V2 = CV1. Through C’ draw a vertical line D’D’.
Solution (b)
- Mark the given point P and join PF1. At F1 draw a line perpendicular to PF1 to cut DD at Q. Join QP and extend it. QP is the tangent at P.
- Through P, draw a line NM perpendicular to QP. NM is the normal at P.
Video Materials For Construction of Ellipse :
Conics – Construction of ellipse
OR
For more Click below ⇓
GE6152 Engineering Graphics Video Lectures