Amplitude Modulation Theory

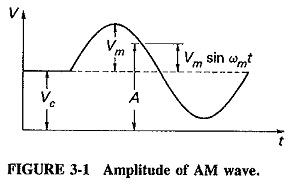
• The process of changing the amplitude of the carrier signal in accordance with the modulating signal transmitted, keeping the frequency and phase of the carrier wave unchanged is known as amplitude modulation. Representation of AM wave:
• 
• The shape of the AM envelope will be the same as that of the information signal or the modulating signal.

Frequency representation of AM wave: (Double sideband – full carrier)

 

Upper sideband:

• The band of the frequency range between f_c and fc+f_m is called as upper sideband(USB).

Lower sideband:

• The band of the frequency range between f_c and fc-f_m is called as lower sideband(LSB).

Upper sideband frequency:

• Any of the frequency that lies between f_c and fc+f_m is called an upper sideband frequency.

Lower sideband frequency:

• Any of the frequency that lies between f_c and fc-f_m is called a lower sideband frequency.

Bandwidth:

• It is the difference between upper sideband frequency to the lower sideband frequency.
• Upper side band frequency = f_c+f
• Lower side band frequency = f_c-f

                                BW= (f_c+f_m) – (f_c-f_m)
Therefore,                BW = 2f_m

 

Coefficient of modulation or modulation index:

• The ratio between the maximum amplitude of the modulating signal to the maximum amplitude of the carrier signal is called a modulation index.
• Modulation index, m= E_m / E_c
• Where E_m be the maximum amplitude of the modulating signal.

                           E_c be the maximum amplitude of the modulating signal.

• Value of E_m must be less than the value of E
• Hence the maximum value of the modulation index will be equal to 1 when E_m = E
• The minimum value will be zero.
• If the modulation index is higher than 1, then it is called overmodulation.

 Percentage of modulation:

• Whenever the coefficient of a modulation index is expressed in terms of percentage then it is called a percentage of modulation.
•   M = (E_m / E_c) *100

Modulation signal:

• Consider the upper highest peak value as V_max=E_m-E_c
• Upper lowest peak value as V_min=E_m-E_c
• Downward highest peak value as -V_max= -E_m-E_c

Downward lowest peak value as -V_min=-E_m+E_c

V_max +V_min = E_m + E_c + E_m – E_c

V_max +V_min = 2 E_m

E_m = (V_max +V_min) / 2

Similarly,

            V_max -V_min = E_m + E_c – E_m + E_c

V_max -V_min = 2 E_c

E_c = (V_max -V_min) / 2

Therefore,

               m= V_m / V_c = E_m / E_c

Therefore,

m= (V_max +V_min) /(V_max -V_min)

M =((V_max +V_min) /(V_max -V_min)) *100

Voltage representation of AM wave: (Equation of double sideband- full carrier)

 From the diagram we can observe the following:

                          v_m(t)=E_m Sin w_mt

where,  v_m(t) be the instantaneous value of the modulating signal.

             E_m be the maximum amplitude of the modulating signal.

             w_m be the angular frequency of the modulating signal.

                            v_c(t)=E_c Sin w_ct

where,  v_c(t) be the instantaneous value of the carrier signal.

             E_c be the maximum amplitude of the carrier signal.

             w_c be the angular frequency of the carrier signal.

Therefore for amplitude modulated signal,

                  V_AM (t) = (E_c + E_m Sin w_mt ) Sin w_ct

                  V_AM (t) = E_c Sin w_ct + E_m Sin w_mt Sin w_ct

                  V_AM (t) = E_cSin w_ct +mE_c Sin w_mt Sin w_ct                  [ since m=E_m / E_c]

                  V_AM (t) = Ec {Sin w_ct +m Sin w_mt Sin w_ct}

                  V_AM (t) = Ec {Sin w_ct +m/2{Cos (w_c-w_m)t – Cos (w_c+w_m)t }}

                              [since SinASinB=1/2(Cos (A-B) – (Cos (A+B))]

                  V_AM (t) = Ec {Sin 2∏f_ct +m/2{Cos 2∏(f_c-f_m)t – Cos 2∏(f_c+f_m)t }}

                  V_AM (t) = Ec Sin 2∏f_ct – mE_c /2{Cos 2∏(f_c+f_m)t – Cos 2∏(f_c-f_m)t }}

• E_c be the amplitude of the carrier signal.
• mE_c/2 be the amplitude of the USB signal.
• mE_c /2 be the amplitude of the LSB signal.
• f_c be the frequency of the carrier signal.
• f_c+f_m be the frequency of the USB signal.
• f_c-f_m be the frequency of the LSB signal

Power distribution of AM wave:

                                          P_c = V_rms²/ load resistor

                              i.e,.      P_c = V_rms²/R

where,                   V_rms be the root mean square voltage.

                               P_c be the power of the carrier signal.

V_rms = V_m / √2 = E_c / √2

                              P_c = (E_c / √2)² /R

P_c = E_c² / 2R

                              P_LSB =  P_USB = (mE_c /2)² / 2R

                              P_LSB =  P_USB = m²E_c² / 8R

                              P_LSB =  P_USB = (m²/4) * (E_c² / 2R)

P_LSB = P_USB = (m²/4) * P_c

Total power           P_T = P_c +P_LSB +P_USB

                                        P_T =P_c+(m²/4) * P_c +(m²/4) * P_c

                              P_T =P_c+2(m²/4) * P_c

                              P_T = P_c+(m²/2) * P_c

                              P_T =P_c( 1+m²/2)

      Where,             m is the modulation index.

                              P_T  is the total power.

                              P_c  is the power of the carrier signal.

Here we providing you general definition and Meaning for the certain topics. To learn or to get notes please visit Analog and Digital Communication Notes