Quadrature Amplitude Modulation
Quadrature amplitude modulation (QAM) is both an analog and a digital modulation scheme. It conveys two analog message signals, or two digital bit streams, by changing (modulating) the amplitudes of two carrier waves, using the amplitude-shift keying (ASK) digital modulation scheme or amplitude modulation (AM) analog modulation scheme. The two carrier waves, usually sinusoids, are out of phase with each other by 90° and are thus called quadrature carriers or quadrature components — hence the name of the scheme. The modulated waves are summed, and the final waveform is a combination of both phase-shift keying (PSK) and amplitude-shift keying (ASK), or (in the analog case) of phase modulation (PM) and amplitude modulation. In the digital QAM case, a finite number of at least two phases and at least two amplitudes are used. PSK modulators are often designed using the QAM principle, but are not considered as QAM since the amplitude of the modulated carrier signal is constant. QAM is used extensively as a modulation scheme for digital telecommunication systems. Arbitrarily high spectral efficiencies can be achieved with QAM by setting a suitable constellation size, limited only by the noise level and linearity of the communications channel.
QAM is being used in optical fiber systems as bit rates increase; QAM16 and QAM64 can be optically emulated with a 3-path interferometer.
Transmitter
The following picture shows the ideal structure of a QAM transmitter, with a carrier frequency  and the frequency response of the transmitter’s filter
and the frequency response of the transmitter’s filter 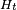 :
:

First the flow of bits to be transmitted is split into two equal parts: this process generates two independent signals to be transmitted. They are encoded separately just like they were in an amplitude-shift keying (ASK) modulator. Then one channel (the one “in phase”) is multiplied by a cosine, while the other channel (in “quadrature”) is multiplied by a sine. This way there is a phase of 90° between them. They are simply added one to the other and sent through the real channel.
The sent signal can be expressed in the form:
where ![\scriptstyle v_c[n]](https://upload.wikimedia.org/math/0/3/c/03cf5d799cb9ed45c8ab9f490da7a9cd.png) and
and ![\scriptstyle v_s[n]](https://upload.wikimedia.org/math/9/6/4/964b261dc3bea178b7bf199aac2ced55.png) are the voltages applied in response to the
are the voltages applied in response to the  th symbol to the cosine and sine waves respectively.
th symbol to the cosine and sine waves respectively.
Receiver
The receiver simply performs the inverse operation of the transmitter. Its ideal structure is shown in the picture below with  the receive filter’s frequency response :
the receive filter’s frequency response :

Multiplying by a cosine (or a sine) and by a low-pass filter it is possible to extract the component in phase (or in quadrature). Then there is only an ASK demodulator and the two flows of data are merged back.
In practice, there is an unknown phase delay between the transmitter and receiver that must be compensated bysynchronization of the receivers local oscillator; i.e., the sine and cosine functions in the above figure. In mobile applications, there will often be an offset in the relative frequency as well, due to the possible presence of a Doppler shift proportional to the relative velocity of the transmitter and receiver. Both the phase and frequency variations introduced by the channel must be compensated by properly tuning the sine and cosine components, which requires a phase reference, and is typically accomplished using a Phase-Locked Loop (PLL).
In any application, the low-pass filter and the receive  filter will be implemented as a single combined filter. Here they are shown as separate just to be clearer.
filter will be implemented as a single combined filter. Here they are shown as separate just to be clearer.

![s(t) = \sum_{n=-\infty}^{\infty} \left[ v_c [n] \cdot h_t (t - n T_s) \cos (2 \pi f_0 t) - v_s[n] \cdot h_t (t - n T_s) \sin (2 \pi f_0 t) \right]](https://upload.wikimedia.org/math/9/5/7/95723e3444ff0900311a74039779ffc0.png)
