Minimum Shift Keying
In digital modulation, minimum-shift keying (MSK) is a type of continuous-phase frequency-shift keying that was developed in the late 1950s and 1960s.Similar to OQPSK, MSK is encoded with bits alternating between quadrature components, with the Q component delayed by half the symbol period. However, instead of square pulses as OQPSK uses, MSK encodes each bit as a half sinusoid. This results in a constant-modulus signal (constant envelope signal), which reduces problems caused by non-linear distortion. In addition to being viewed as related to OQPSK, MSK can also be viewed as a continuous phase frequency shift keyed (CPFSK) signal with a frequency separation of one-half the bit rate.
In MSK the difference between the higher and lower frequency is identical to half the bit rate. Consequently, the wave forms used to represent a 0 and a 1 bit differ by exactly half a carrier period. Thus, the maximum frequency deviation is  = 0.25 fm where fm is the maximum modulating frequency. As a result, the modulation index m is 0.5. This is the smallest FSK modulation index that can be chosen such that the wave forms for 0 and 1 are orthogonal. A variant of MSK called GMSK is used in the GSM mobile phone standard.
= 0.25 fm where fm is the maximum modulating frequency. As a result, the modulation index m is 0.5. This is the smallest FSK modulation index that can be chosen such that the wave forms for 0 and 1 are orthogonal. A variant of MSK called GMSK is used in the GSM mobile phone standard.
Mathematical representation
The resulting signal is represented by the formula 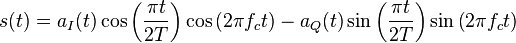
where  and
and 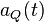 encode the even and odd information respectively with a sequence of square pulses of duration 2T.
encode the even and odd information respectively with a sequence of square pulses of duration 2T.  has its pulse edges on
has its pulse edges on ![t=[-T,T,3T,...]](https://upload.wikimedia.org/math/6/8/3/683af0b06364ca631c2acfbf89be2516.png) and
and 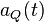 on
on ![t=[0,2T,4T,...]](https://upload.wikimedia.org/math/d/2/c/d2c483750fea33087d27f6abd6255539.png) . The carrier frequency is
. The carrier frequency is 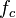 .
.
Using the trigonometric identity, this can be rewritten in a form where the phase and frequency modulation are more obvious,
![<br /> s(t) = \cos\left[2 \pi f_c t + b_k(t) \frac{\pi t}{2 T} + \phi_k\right]<br />](https://upload.wikimedia.org/math/c/2/7/c27a6dce9d79fc1a62450bcc94e80194.png)
where bk(t) is +1 when  and -1 if they are of opposite signs, and
and -1 if they are of opposite signs, and  is 0 if
is 0 if  is 1, and
is 1, and 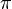 otherwise. Therefore, the signal is modulated in frequency and phase, and the phase changes continuously and linearly.
otherwise. Therefore, the signal is modulated in frequency and phase, and the phase changes continuously and linearly.

