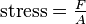Stress Strain Relationship
Stress
Stress is “force per unit area” – the ratio of applied force F and cross section – defined as “force per area”.
- tensile stress – stress that tends to stretch or lengthen the material – acts normal to the stressed area
- compressive stress – stress that tends to compress or shorten the material – acts normal to the stressed area
- shearing stress – stress that tends to shear the material – acts in plane to the stressed area at right-angles to compressive or tensile stress
Strain
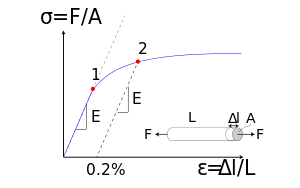
Strain is defined as “deformation of a solid due to stress” and can be expressed as
ε = dl / lo
= σ / E
where
dl = change of length (m, in)
lo = initial length (m, in)
ε = unit less measure of engineering strain
E = Young’s modulus (Modulus of Elasticity) (N/m2 (Pa), lb/in2 (psi))
- Young’s modulus can be used to predict the elongation or compression of an object.
Stress Strain Relationship:
The relationship between the stress and strain that a particular material displays is known as that particular material’s stress–strain curve. It is unique for each material and is found by recording the amount of deformation (strain) at distinct intervals of tensile or compressive loading (stress). These curves reveal many of the properties of a material (including data to establish the Modulus of Elasticity, E).
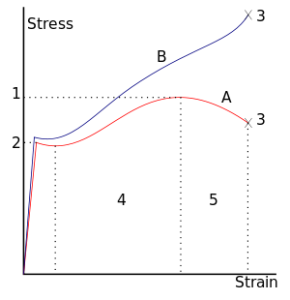
Stress Vs Strain Diagram
Stress–strain curves of various materials vary widely, and different tensile tests conducted on the same material yield different results, depending upon the temperature of the specimen and the speed of the loading. It is possible, however, to distinguish some common characteristics among the stress–strain curves of various groups of materials and, on this basis, to divide materials into two broad categories; namely, the ductile materials and the brittle materials.
Consider a bar of cross sectional area A being subjected to equal and opposite forces F pulling at the ends so the bar is under tension. The material is experiencing a stress defined to be the ratio of the force to the cross sectional area of the bar:
This stress is called the tensile stress because every part of the object is subjected to tension. The SI unit of stress is the newton per square meter, which is called the pascal.
1 pascal = 1 Pa = 1 N/m2
Now consider a force that is applied tangentially to an object. The ratio of the shearing force to the area A is called the shear stress.
If the object is twisted through an angle q, then the shear strain is:
shear strain = tan q
Finally, the shear modulus MS of a material is defined as the ratio of shear stress to shear strain at any point in an object made of that material. The shear modulus is also known as the torsion modulus.