Principles of Isometric Projection
What is Isometric Projection?
Iso (in Greek) means equal; metric means to measure. Hence Isometric projection means a system of projection of equality of measure.
Orthographic Projection of a cube: The principle involved in drawing an isometric projection can be explained best by drawing the Orthographic Projection of a Cube, resting on HP on one of its corners with a solid diagonal (solid diagonal is an imaginary line joining one of the corners at the top and the diametrically opposite corner at the bottom) perpendicular to HP.
Isometric Projection: 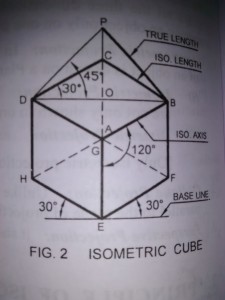 The diagram shows the top view of the cube, obtained from the Orthographic projection. It gives a fair idea of a pictorial form of the cube and its Isometric Projection.
The diagram shows the top view of the cube, obtained from the Orthographic projection. It gives a fair idea of a pictorial form of the cube and its Isometric Projection.
- All the edges and faces of the cube are equally inclined to the plane of projection. Hence the square faces are seen as similar and equal rhombuses.
- The three edges/sides of the cube AB, AD and AE are meeting at the point A. These edges are mutually perpendicular to each other in the solid.
- Above three edges from 90º in the Orthographic Projection and are now seen to include 120º with each other in Isometric Projection.
- Edges AB and AD make 30º with the horizontal. Edge AE is vertical.
- The three edges AB, AD and AE meeting at A forming a right angle are also equally inclined to VP and therefore they are equally foreshortened.
All the other edges like CB and BF are parallel to any of the lines AB, AD, AE and are also equally foreshortened. These edges being equally foreshortened leads us to the problem of selecting an Isometric scale. - BD and AC represent equal diagonals of the cube but are equally shortened in Isometric view. Diagonal DA of the top face of the cube is parallel to the VP. Hence it retains its true length in Isometric. However, the diagonal AC is shortened.

