Population Inversion
In science, specifically statistical mechanics, a population inversion occurs while a system (such as a group of atoms or molecules) exists in a state with more members in an excited state than in lower energy states. It is called an “inversion” because in many familiar and commonly encountered physical systems, this is not possible. The concept is of fundamental importance in laser science because the production of a population inversion is a necessary step in the workings of a standard laser.
Creating a population inversion
As described above, a population inversion is required for laser operation, but cannot be achieved in our theoretical group of atoms with two energy-levels when they are in thermal equilibrium. In fact, any method by which the atoms are directly and continuously excited from the ground state to the excited state (such as optical absorption) will eventually reach equilibrium with the de-exciting processes of spontaneous and stimulated emission. At best, an equal population of the two states, N1 =N2 = N/2, can be achieved, resulting in optical transparency but no net optical gain.
Three-level lasers
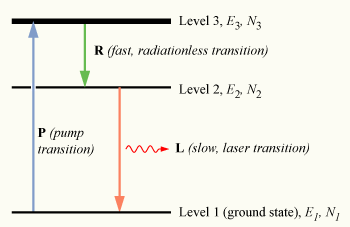
To achieve non-equilibrium conditions, an indirect method of populating the excited state must be used. To understand how this is done, we may use a slightly more realistic model, that of a three-level laser. Again consider a group of N atoms, this time with each atom able to exist in any of three energy states, levels 1, 2 and 3, with energies E1, E2, and E3, and populations N1,N2, and N3, respectively.
We assume that E1 < E2 < E3; that is, the energy of level 2 lies between that of the ground state and level 3.
Initially, the system of atoms is at thermal equilibrium, and the majority of the atoms will be in the ground state, i.e., N1 ≈ N, N2≈ N3 ≈ 0. If we now subject the atoms to light of a frequency 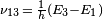 , the process of optical absorption will excite the atoms from the ground state to level 3. This process is called pumping and does not necessarily always directly involve light absorption; other methods of exciting the laser medium, such as electrical discharge or chemical reactions, may be used. The level 3 is sometimes referred to as the pump level or pump band, and the energy transition E1 → E3 as the pump transition, which is shown as the arrow marked P in the diagram on the right.
, the process of optical absorption will excite the atoms from the ground state to level 3. This process is called pumping and does not necessarily always directly involve light absorption; other methods of exciting the laser medium, such as electrical discharge or chemical reactions, may be used. The level 3 is sometimes referred to as the pump level or pump band, and the energy transition E1 → E3 as the pump transition, which is shown as the arrow marked P in the diagram on the right.
If we continuously pump the atoms, we will excite an appreciable number of them into level 3, such that N3 > 0. To have a medium suitable for laser operation, it is necessary that these excited atoms to quickly decay to level 2. The energy released in this transition may be emitted as a photon (spontaneous emission), however in practice the 3→2 transition (labeled R in the diagram) is usually radiationless, with the energy being transferred to vibrational motion (heat) of the host material surrounding the atoms, without the generation of a photon.
An atom in level 2 may decay by spontaneous emission to the ground state, releasing a photon of frequency ν12 (given byE2 – E1 = hν12), which is shown as the transition L, called the laser transition in the diagram. If the lifetime of this transition, τ21 is much longer than the lifetime of the radiationless 3 → 2 transition τ32 (if τ21 ≫ τ32, known as a favourable lifetime ratio), the population of the E3 will be essentially zero (N3 ≈ 0) and a population of excited state atoms will accumulate in level 2 (N2> 0). If over half the N atoms can be accumulated in this state, this will exceed the population of the ground state N1. A population inversion (N2 > N1 ) has thus been achieved between level 1 and 2, and optical amplification at the frequency ν21can be obtained.
Because at least half the population of atoms must be excited from the ground state to obtain a population inversion, the laser medium must be very strongly pumped. This makes three-level lasers rather inefficient, despite being the first type of laser to be discovered (based on a ruby laser medium, by Theodore Maiman in 1960). A three-level system could also have a radiative transition between level 3 and 2, and a non-radiative transition between 2 and 1. In this case, the pumping requirements are weaker. In practice, most lasers are four-level lasers, described below.
Four-level lasers[edit]

Here, there are four energy levels, energies E1, E2, E3, E4, and populations N1, N2, N3, N4, respectively. The energies of each level are such that E1 < E2 < E3 < E4.
In this system, the pumping transition P excites the atoms in the ground state (level 1) into the pump band (level 4). From level 4, the atoms again decay by a fast, non-radiative transition Rainto the level 3. Since the lifetime of the laser transition L is long compared to that of Ra (τ32 ≫ τ43), a population accumulates in level 3 (the upper laser level), which may relax by spontaneous or stimulated emission into level 2 (the lower laser level). This level likewise has a fast, non-radiative decay Rb into the ground state.
As before, the presence of a fast, radiationless decay transition results in the population of the pump band being quickly depleted (N4 ≈ 0). In a four-level system, any atom in the lower laser level E2 is also quickly de-excited, leading to a negligible population in that state (N2 ≈ 0). This is important, since any appreciable population accumulating in level 3, the upper laser level, will form a population inversion with respect to level 2. That is, as long as N3 > 0, then N3 > N2 and a population inversion is achieved. Thus optical amplification, and laser operation, can take place at a frequency of ν32 (E3–E2= hν32).
Since only a few atoms must be excited into the upper laser level to form a population inversion, a four-level laser is much more efficient than a three-level one, and most practical lasers are of this type. In reality, many more than four energy levels may be involved in the laser process, with complex excitation and relaxation processes involved between these levels. In particular, the pump band may consist of several distinct energy levels, or a continuum of levels, which allow optical pumping of the medium over a wide range of wavelengths.
Note that in both three- and four-level lasers, the energy of the pumping transition is greater than that of the laser transition. This means that, if the laser is optically pumped, the frequency of the pumping light must be greater than that of the resulting laser light. In other words, the pump wavelength is shorter than the laser wavelength. It is possible in some media to use multiple photon absorptions between multiple lower-energy transitions to reach the pump level; such lasers are calledup-conversion lasers.
While in many lasers the laser process involves the transition of atoms between different electronic energy states, as described in the model above, this is not the only mechanism that can result in laser action. For example, there are many common lasers (e.g., dye lasers, carbon dioxide lasers) where the laser medium consists of complete molecules, and energy states correspond to vibrational and rotational modes of oscillation of the molecules. This is the case with water masers, that occur in nature.
In some media it is possible, by imposing an additional optical or microwave field, to use quantum coherence effects to reduce the likelihood of an excited-state to ground-state transition. This technique, known as lasing without inversion, allows optical amplification to take place without producing a population inversion between the two states.

