Poisson’s ratio
Poisson’s ratio is the ratio of transverse contraction strain to longitudinal extension strain in the direction of stretching force. Tensile deformation is considered positive and compressive deformation is considered negative. The definition of Poisson ratio contains a minus sign so that normal materials have a positive ratio. Poisson’s ratio, also called Poisson ratio or the Poisson coefficient, or coefficient de Poisson is usually represented as a lower case Greek nu, n.
n = – etrans / elongitudinal
Strain e is defined in elementary form as the change in length divided by the original length.
e = DL/L.
Poisson’s ratio:
Virtually all common materials, such as the blue rubber band on the right, become narrower in cross-section when they are stretched. The reason why, in the continuum view, is that most materials resist a change in volume as determined by the bulk modulus K more than they resist a change in shape, as determined by the shear modulus G.
In the structural view, the reason for the usual positive Poisson ratio is that inter-atomic bonds realign with deformation. The stretching of the yellow honeycomb by vertical forces, shown on the right, illustrates the concept.
Poisson ratio: relation to elastic moduli in isotropic solids
Poisson’s ratio is related to elastic moduli K (also called B), the bulk modulus; G as the shear modulus; and E, Young’s modulus, by the following (for isotropic solids, those for which properties are independent of direction). The elastic moduli are measures of stiffness. They are ratios of stress to strain. Stress is force per unit area, with the direction of both the force and the area specified.
n = (3K – 2G)/(6K + 2G)
E = 2G( 1 + n)
E = 3K(1 – 2 n)
Further interrelations among elastic constants for isotropic solids are as follows. B is the bulk modulus.
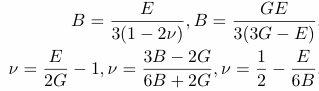
Elasticity interrelations with Poisson ratio 1
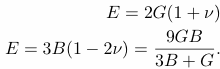
Elasticity interrelations with Poisson ratio 2
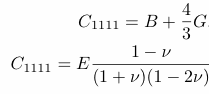
Elasticity interrelations with Poisson ratio 3
The theory of isotropic linear elasticity allows Poisson’s ratios in the range from -1 to 1/2 for an object with free surfaces with no constraint. Physically the reason is that for the material to be stable, the stiffnesses must be positive; the bulk and shear stiffnesses are interrelated by formulae which incorporate Poisson ratio. Objects constrained at the surface can have a Poisson’s ratio outside the above range and be stable.

