Physical significance of wave function
A wave function is a mathematical tool used in quantum mechanics to describe any physical system. It is a function from a space that maps the possible states of the system into the complex numbers. The laws of quantum mechanics (i.e. the Schrödinger equation) describe how the wave function evolves over time. The values of the wave function are probability amplitudes — complex numbers — the squares of the absolute values of which give the probability distribution that the system will be in any of the possible states.
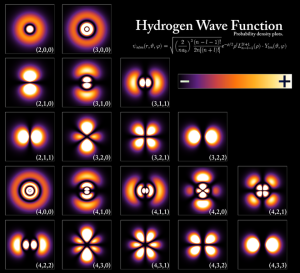
Physical significance of wave function
The electron probability density for the first few hydrogen atom electron orbitals shown as cross-sections. These orbitals form an orthonormal basis for the wave function of the electron.
It is commonly applied as a property of particles relating to their wave-particle duality, where it is denotedψ(position,time) and where | ψ | 2 is equal to the chance of finding the subject at a certain time and position.For example, in an atom with a single electron, such as hydrogen or ionized helium, the wave function of the electron provides a complete description of how the electron behaves. It can be decomposed into a series ofatomic orbitals which form a basis for the possible wave functions. For atoms with more than one electron (or any system with multiple particles), the underlying space is the possible configurations of all the electrons and the wave function describes the probabilities of those configurations.
Definition: The modern usage of the term wave function refers to a complex vector or function, i.e. an element in a complex Hilbert space. Typically, a wave function is either:
- a complex vector with finitely many components
 ,
,
- a complex vector with infinitely many components
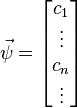 ,
,
- a complex function of one or more real variables (a continuously indexed complex vector)
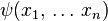 .
.
