One Component System
For pure substances C = 1 so that F = 3 – P. In a single phase (P = 1) condition of a pure component system, two variables (F = 2), such as temperature and pressure, can be chosen independently to be any pair of values consistent with the phase. However, if the temperature and pressure combination ranges to a point where the pure component undergoes a separation into two phases (P = 2), F decreases from 2 to 1. When the system enters the two-phase region, it becomes no longer possible to independently control temperature and pressure.
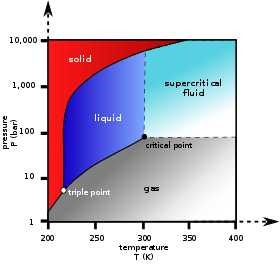
Carbon dioxide pressure-temperature phase diagram showing the triple point and critical point of carbon dioxide
In the phase diagram to the right, the boundary curve between the liquid and gas regions maps the constraint between temperature and pressure when the single-component system has separated into liquid and gas phases at equilibrium. If the pressure is increased by compression, some of the gas condenses and the temperature goes up. If the temperature is decreased by cooling, some of the gas condenses, decreasing the pressure. Throughout both processes, the temperature and pressure stay in the relationship shown by this boundary curve unless one phase is entirely consumed by evaporation or condensation, or unless the critical point is reached. As long as there are two phases, there is only one degree of freedom, which corresponds to the position along the phase boundary curve.
The critical point is the black dot at the end of the liquid–gas boundary. As this point is approached, the liquid and gas phases become progressively more similar until, at the critical point, there is no longer a separation into two phases. Above the critical point and away from the phase boundary curve, F = 2 and the temperature and pressure can be controlled independently. Hence there is only one phase, and it has the physical properties of a dense gas, but is also referred to as a supercritical fluid.
Of the other two-boundary curves, one is the solid–liquid boundary or melting point curve which indicates the conditions for equilibrium between these two phases, and the other at lower temperature and pressure is the solid–gas boundary.
Even for a pure substance, it is possible that three phases, such as solid, liquid and vapour, can exist together in equilibrium (P = 3). If there is only one component, there are no degrees of freedom (F = 0) when there are three phases. Therefore, in a single-component system, this three-phase mixture can only exist at a single temperature and pressure, which is known as a triple point. Here there are two equations μsol(T, p) = μliq(T, p) = μvap(T, p), which are sufficient to determine the two variables T and p. In the diagram for CO2 the triple point is the point at which the solid, liquid and gas phases come together, at 5.2 bar and 217 K. It is also possible for other sets of phases to form a triple point, for example in the water system there is a triple point where ice I, ice III and liquid can coexist.
If four phases of a pure substance were in equilibrium (P = 4), the phase rule would give F = −1, which is meaningless, since there cannot be −1 independent variables. This explains the fact that four phases of a pure substance (such as ice I, ice III, liquid water and water vapour) are not found in equilibrium at any temperature and pressure. In terms of chemical potentials there are now three equations, which cannot in general be satisfied by any values of the two variables T and p, although in principle they might be solved in a special case where one equation is mathematically dependent on the other two. In practice, however, the coexistence of more phases than allowed by the phase rule normally means that the phases are not all in true equilibrium.

