Maxwell relations
The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of differentiation of an analytic function of two variables is irrelevant. If Φ is a thermodynamic potential and xi and xj are two different natural variables for that potential, then the Maxwell relation for that potential and those variables is:
-
Maxwell relations 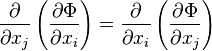
where the partial derivatives are taken with all other natural variables held constant. It is seen that for every thermodynamic potential there are n(n − 1)/2 possible Maxwell relations where n is the number of natural variables for that potential.
The four most common Maxwell relations are the equalities of the second derivatives of each of the four thermodynamic potentials, with respect to their thermal natural variable (temperature T; or entropy S) and theirmechanical natural variable (pressure P; or volume V):
-
Maxwell’s relations (common) 
where the potentials as functions of their natural thermal and mechanical variables are the internal energy U(S, V), enthalpyH(S, P), Helmholtz free energy F(T, V) and Gibbs free energy G(T, P). The thermodynamic square can be used as amnemonic to recall and derive these relations.

