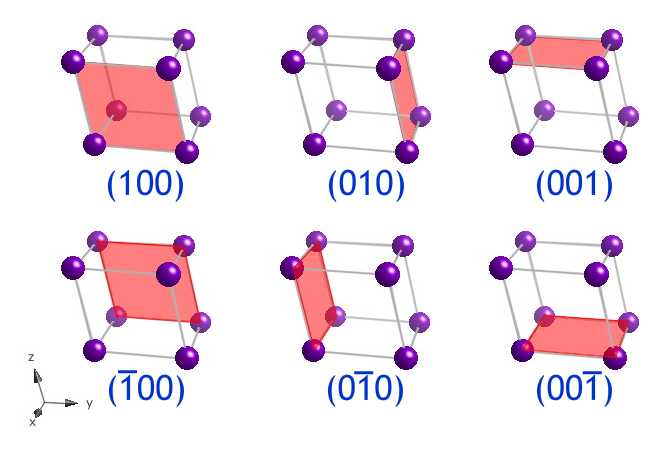
Lattice Plane
In crystallography, a lattice plane of a given Bravais lattice is a plane (or family of parallel planes) whose intersections with the lattice (or any crystalline structure of that lattice) are periodic (i.e. are described by 2d Bravais lattices) and intersect the Bravais lattice; equivalently, a lattice plane is any plane containing at least three noncollinear Bravais lattice points. All lattice planes can be described by a set of integer Miller indices, and vice versa (all integer Miller indices define lattice planes).
Conversely, planes that are not lattice planes have aperiodic intersections with the lattice called quasicrystals; this is known as a “cut-and-project” construction of a quasicrystal (and is typically also generalized to higher dimensions).
To gain more knowledge about hardware and software just click here
You can share your feedback (both positive and negative) by mailing to [email protected]. It will help us to improve our site.We will respond your mail within 24 hours.