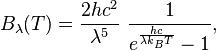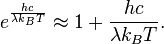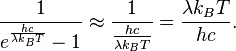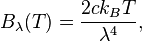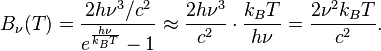Jeans Law from Planck’s theory

In physics, the Rayleigh Jeans law attempts to describe the spectral radiance of electromagnetic radiation at all wavelengths from a black body at a given temperature through classical arguments. For wavelength λ, it is:

Jeans Law from Planck’s theory

where c is the speed of light, $k B$ is the Boltzmann constant and T is the temperature in kelvins. For frequency ν, the expression is instead

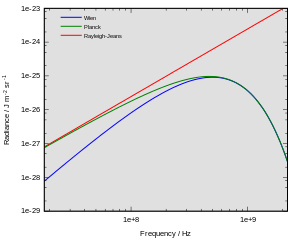
Jeans Law from Planck’s theory

The Rayleigh Jeans law agrees with experimental results at large wavelengths (low frequencies) but strongly disagrees at short wavelengths (high frequencies). This inconsistency between observations and the predictions of classical physics is commonly known as the ultraviolet catastrophe, and its resolution was a foundational aspect of the development of quantum mechanics in the early 20th century.

jeans law

Comparison to Planck’s law

In 1900 Max Planck empirically obtained an expression for black-body radiation expressed in terms of wavelength λ = c/ν(Planck’s law):

B_\lambda(T) = \frac{2 h c^2}{\lambda^5}~\frac{1}{e^\frac{hc}{\lambda k_B T}-1},

where h is the Planck constant and $k B$ the Boltzmann constant. The Planck law does not suffer from an ultraviolet catastrophe, and agrees well with the experimental data, but its full significance (which ultimately led to quantum theory) was only appreciated several years later. Since,

e^x = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + \cdots.

then in the limit of very high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the Taylor polynomial’s first-order term,

e^{\frac{hc}{\lambda k_B T}} \approx 1 + \frac{hc}{\lambda k_B T}.

So,

\frac{1}{e^\frac{hc}{\lambda k_B T}-1} \approx \frac{1}{\frac{hc}{\lambda k_B T}} = \frac{\lambda k_B T}{hc}.

This results in Planck’s blackbody formula reducing to

B_{\lambda}(T) = \frac{2ck_B T}{\lambda^4},

which is identical to the classically derived Rayleigh–Jeans expression.

The same argument can be applied to the blackbody radiation expressed in terms of frequency ν = c/λ. In the limit of small frequencies, that is $h \nu \ll k_B T$ ,