Construction of Hypocycloid

Sample Problem 1:
Draw a Hypocycloid of a circle of 40mm diameter which rolls inside another circle of 200mm diameter for one revolution. Draw a tangent and normal at any point on it.

Steps for construction of Hypocycloid:

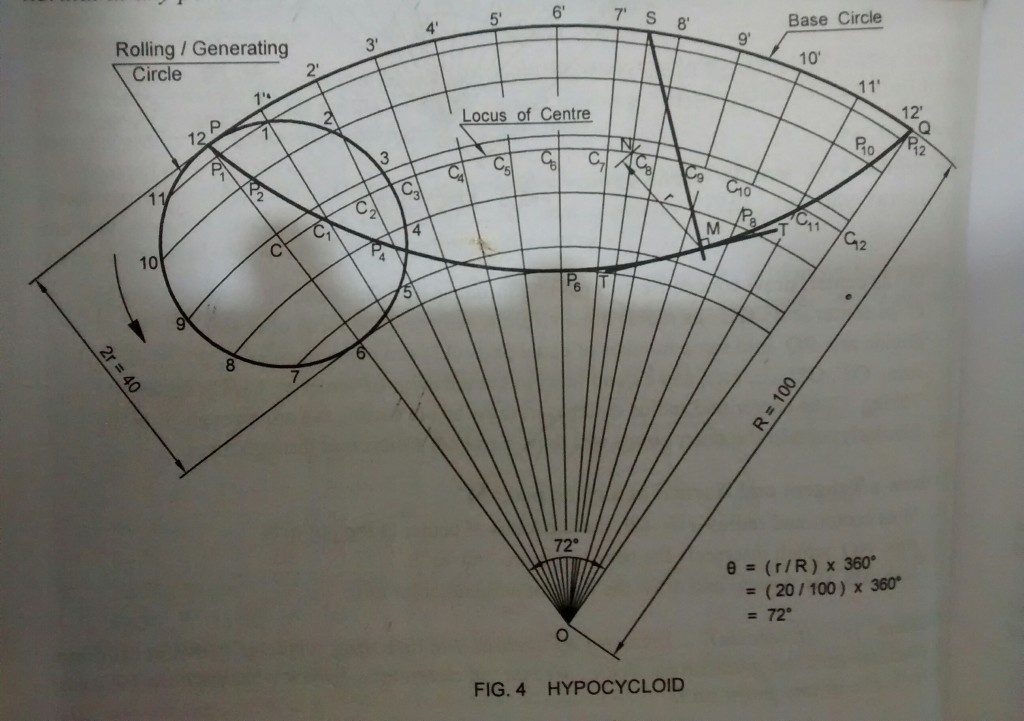
1. To calculate θ : θ=r/R * 360º = 20/100 * 360º = 72°.
2. Taking any point O as center and radius (R) 100mm, draw an arc PQ which subtends an angle θ = 72º at O.
3. Let P be the generating point. On OP mark PC = r = 20mm = radius of rolling circle.
4. With C as center and radius r (20mm) draw the rolling circle.
5. Divide the rolling circle into 12 equal parts as 1,2,3,etc., in CM direction, since the rolling circle is assumed to roll CCW.
6. Repeat Step Nos. 5 to 10 in problem 6 and draw a smooth Hypocycloid curve.
   Tangent and Normal at a given point M.
7. M as center and radius r=CP cut the locus of center at the point N.
8. Join ON and extend it to intersect the base circle at S.
9. Join MS, the Normal.
10. At M, draw a line perpendicular to MS to get the required Tangent.

Video lecture of Construction of Hypocycloid

Construction of Hypocycloid