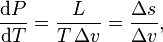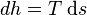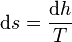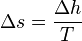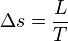Clausius-Clapeyron Equation

The Clausius–Clapeyron relation, named after Rudolf Clausius and Benoît Paul Émile Clapeyron, is a way of characterizing a discontinuous phase transition between two phases of matter of a single constituent. On a pressure–temperature (P–T) diagram, the line separating the two phases is known as the coexistence curve. The Clausius–Clapeyron relation gives the slope of the tangents to this curve. Mathematically,

where 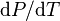is the slope of the tangent to the coexistence curve at any point, is the specific latent heat, is the temperature, 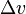is the specific volume change of the phase transition and 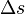is the entropy change of the phase transition.

Derivation from state postulate

Using the state postulate, take the specific entropy for a homogeneous substance to be a function of specific volume and temperature .

The Clausius–Clapeyron relation characterizes behavior of a closed system during a phase change, during which temperature and pressureare constant by definition. Therefore,^[3]:508

Using the appropriate Maxwell relation gives

where 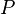is the pressure. Since pressure and temperature are constant, by definition the derivative of pressure with respect to temperature does not change.^{[4][5]:57, 62 & 671} Therefore the partial derivative of specific entropy may be changed into atotal derivative

and the total derivative of pressure with respect to temperature may be factored out when integrating from an initial phase to a final phase , to obtain

where 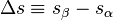and 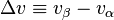are respectively the change in specific entropy and specific volume. Given that a phase change is an internally reversible process, and that our system is closed, the first law of thermodynamics holds

where is the internal energy of the system. Given constant pressure and temperature (during a phase change) and the definition of specific enthalpy 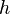, we obtain

Given constant pressure and temperature (during a phase change), we obtain

Substituting the definition of specific latent heat 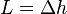gives

Substituting this result into the pressure derivative given above (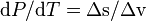), we obtain

This result (also known as the Clapeyron equation) equates the slope of the tangent to the coexistence curve 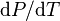, at any given point on the curve, to the function 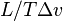of the specific latent heat , the temperature , and the change in specific volume 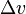.