introduction to decimal number system
Decimal number system, also called Hindu-Arabic, or Arabic, number system, in mathematics, positional numeral system employing 10 as the base and requiring 10 different numerals, the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. It also requires a dot (decimal point) to represent decimal fractions. In this scheme, the numerals used in denoting a number take different place values depending upon position. In a base-10 system the number 543.21 represents the sum (5 × 102) + (4 × 101) + (3 × 100) + (2 × 10−1) + (1 × 10−2).
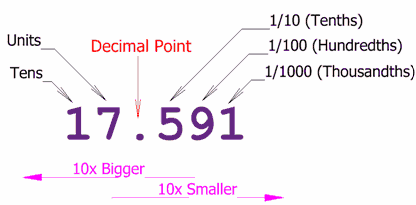
Decimal number system
DECIMAL NUMBER CONVERSIONS:

decimal to binary conversion

decimal to octal conversion

decimal to hexadecimal conversion
Decimal to Other Base System
Steps:
- Step 1 – Divide the decimal number to be converted by the value of the new base.
- Step 2 – Get the remainder from Step 1 as the rightmost digit (least significant digit) of new base number.
- Step 3 – Divide the quotient of the previous divide by the new base.
- Step 4 – Record the remainder from Step 3 as the next digit (to the left) of the new base number.
Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3.
The last remainder thus obtained will be the most significant digit (MSD) of the new base number.
Some important number systems are as follows.
樂威壯
align: left;”>

